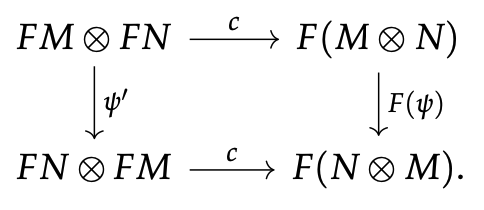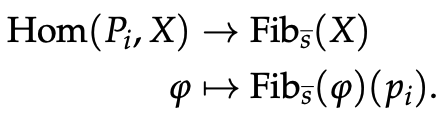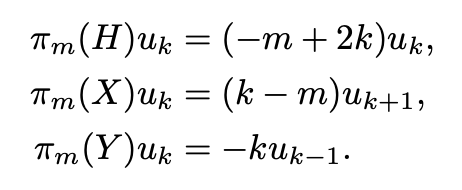General writings
Recent-ish notes
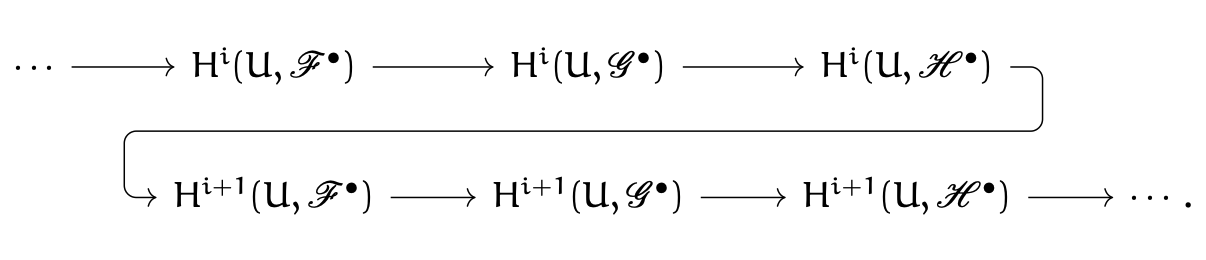
Notes of Everything
Notes about commutative / homological algebra, sheaf theory and algebraic geometry. In the future this ought to be a comprehensive introduction to algebraic geometry. (Work in progress.)
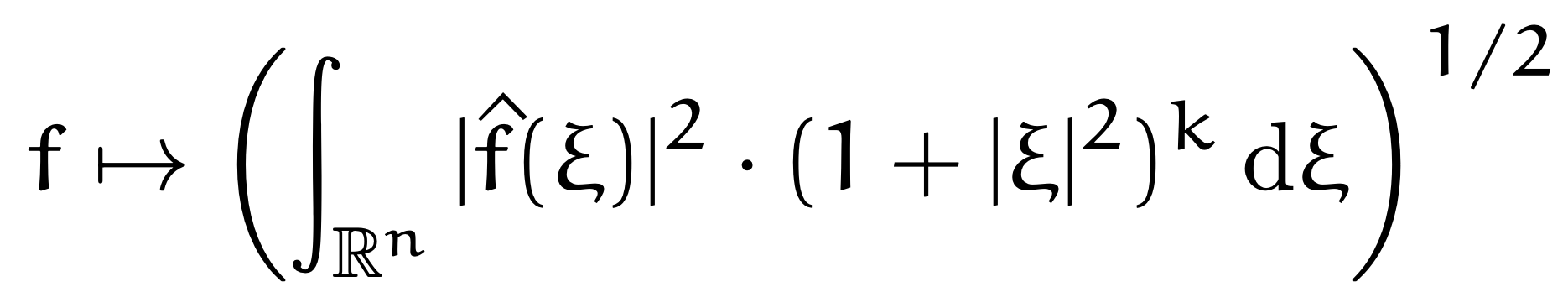
The Hodge decomposition
The Hodge decomposition follows directly from a basic result on elliptic differential operators. This result is usually treated as a black-box in a lot of references. The goal of these notes is to demystify its proof.
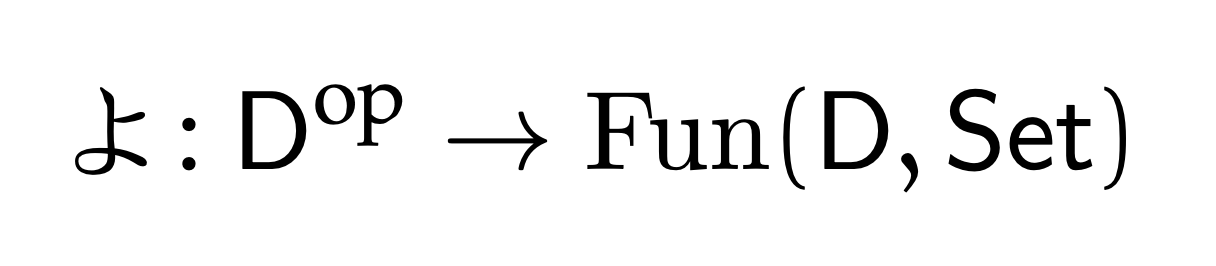
Adjoints can be defined on objects
Little notes explaining a surprisingly not-so-well-known corollary of the Yoneda lemma, which says that we can define an adjoint functor by only specifying how it acts on objects.
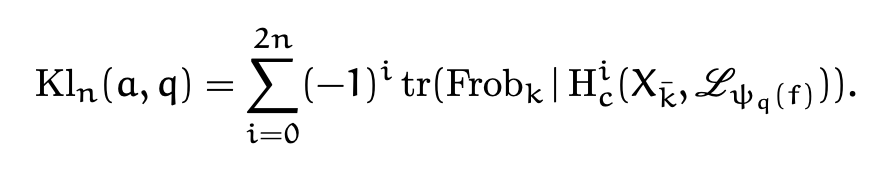
Exponential Sums: a tour through number theory
We use exponential sums as "an excuse" to learn lots of interesting ideas in number theory and algebraic geometry. These notes were strongly influenced by N. Katz course in Orsay and by J. Fresán Séminaire Bourbaki on the subject.
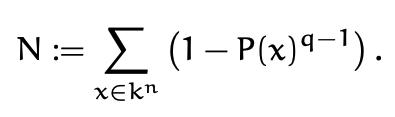
Wedderburn's Little Theorem
Quick notes about a very beautiful proof of the fact that a finite division ring is commutative using the Chevalley-Warning theorem (which is incredible by itself).
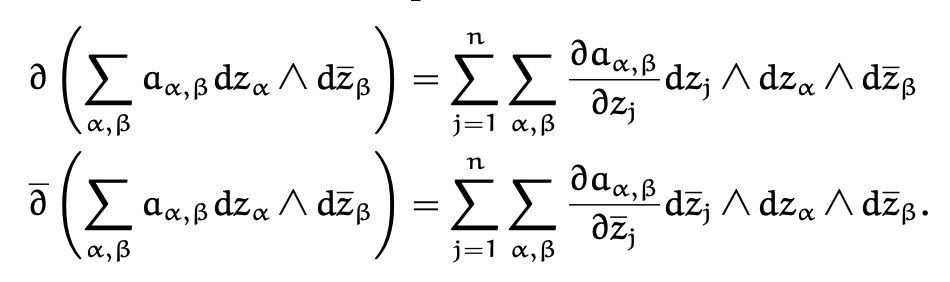
Complex Geometry
These notes contain a (very) brief introduction to complex analysis in one and several variables, and begin to explain some concepts of complex geometry. The first chapter is mostly done but the rest is quite rough. So caveat emptor.